Graph 활용-1

출처 엔지니어 대한민국

문제 1. Graph에서 두지점의 경로찾기

그래프에서 두 개의 노드가 서로 찾아갈 수 있는 경로가 있는지 확인하는 함수를 구현해보자 그래프에서 특정 노드 A와 B를 잇는 간선의 존재 여부를 판단하는 메서드이다.

 

DFS와 BFS 두 가지 방법 모두 경로를 찾을수 있지만 이런 문제의 경우 시작점을 기준으로 영역을 점차 넓히며 접근하는게 조금 더 빠른 방법일 수 있기 때문에 BFS, 넓이 우선 탐색을 사용해 접근한다.

구현

import java.util.LinkedList; 
import java.util.Iterator; 
import java.util.NoSuchElementException;  

class Queue<T>{ }  

class Graph{ 	
	class Node{     	
    	int data;         
        // 인접한 노드들과의 관계         
        LinkedList<Node> adjacent;         
        // 방문했는지 마킹         
        boolean marked;                  
        //Node 생성자         
        Node (int data){         	
        	this.data = data;             
            this.marked = false;             
            adjacent = new LinkedList<Node>();         
         } 	
      }          
     
     Node[] nodes; // node들을 저장할 배열     
     Graph(int size){     	
     	nodes = new Node[size];         
        for(int i=0; i<size; i++){         	
        	nodes[i] = new Node(i);         
            }     
         }        
         
        //두 노드의 관계를 저장     
        void addEdge(int i1, int i2){     	
        	Node n1 = nodes[i1];         
            Node n2 = nodes[i2];                  
            //상대방이 있는지 확인하고 없으면 추가         
            if(!n1.adjacent.contains(n2)){         	
            	n1.adjacent.add(n2);         
                }         
            if(!n2.adjacent.contains(n1)){         	
            	n2.adjacent.add(n1);         
                }     
         }          
         // 검색전 모든 Making Flag를 false로 초기화하는 메서드     
         void initMarks(){       
         	for (Node n : nodes) {           
            	n.marked = false;	       
                } 	
          }          
          
         // 배열 인덱스로 호출하면 노드로 변환해서 호출하는 함수     
         
         boolean search(int i1, int i2) {     	
         	return search(nodes[i1], nodes[i2]);     
         }          
         
         // start와 end Node를 받는 두 개의 노드 경로를 확인하는 함수     
         boolean search(Node start, Node end){     	
         	initMarks();         
            LinkedList<Node> q = new LinkedList<Node>();         
            q.add(start);         
            while(!q.isEmpty()){           
            	Node root = q.removeFirst();           
                if(root == end){               
                	return true;           
                }           
            for(Node n : root.adjacent) {           	
             	if(n.marked == false){             	
                	n.marked = true;                 
                    q.add(n);             
                 }           
             }         
          }         
          return false;     
      }          
      public class Test {     	
      	public static void main(String[] args){         	
        	Graph g = new Graph(9);             
            g.addEdge(0,1);             
            g.addEdge(1,2);             
            g.addEdge(1,3);             
            g.addEdge(2,4);             
            g.addEdge(3,4);             
            g.addEdge(3,5);             
            g.addEdge(5,6);             
            g.addEdge(5,7);             
            g.addEdge(6,8); 
  
  /*         0        
  			/       
           1 ㅡㅡ3    7       
           |  / | \ /       
           | /  |  5       
           2ㅡㅡ4   \                 
           			6ㅡ8 
   */ 			
   			System.out.println(g.search(1,8));         
        }     
  }

search(Node start, Node end) 함수는 먼저 start 노드를 큐에 담고 인접한 노드를 하나씩 추가하고 end 노드와 비교하며 일치 여부를 판단하는 메서드이다.

모든 노드를 탐색하며 진행하는데 이 때 탐색이 끝났음에도 return 되지 않는다면 false를 반환하며 종료된다.

---

문제 2. 배열을 이진 검색 트리로 만들기

정렬이 되어 있고, 고유한 정수로만 이루어진 배열이 있다. 이 배열로 이진 검색 트리를 구현하시오.

 

배열이 정렬되어있는 상태이고, 배열의 데이터가 고유하기 때문에 배열의 가운데에 있는 숫자를 보고 검색하고자 하는 숫자보다 크면 오른쪽으로, 작으면 왼쪽으로 찾아 들어가는 방법을 통해 접근할 수 있다.

 

만약 배열이 짝수로 존재한다면, 딱 떨어지는 중간 값이 없기 때문에 앞에 있는 숫자를 중간 값으로 취급하는 조건을 달아준다.

int[] arr = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 

이진 검색 트리(Binary Search Tree)는 모든 노드가 최대 두 개의 자식 노드를 가지면서, 왼쪽 자식 노드는 현재 노드보다 작은 값을, 오른쪽 자식 노드는 현재 노드보다 큰 값을 가지는 트리이다.

 

이진 검색 트리에서 특정 값을 검색하는 경우, 루트 노드부터 시작하여 찾고자 하는 값이 현재 노드보다 작으면 왼쪽 자식 노드를 탐색하고, 크면 오른쪽 자식 노드를 탐색하며 이 과정을 반복하여 값을 찾는다.

 

따라서, 위 와 같은 arr 배열이 존재하고 이를 이진 검색 트리로 만든다면 다음과 같은 과정을 갖는다.

1. 배열 arr의 중앙에 위치한 값을 기준으로 루트 노드를 생성한다.
2. 루트 노드의 왼쪽 서브트리는 arr의 왼쪽 절반을 이진 검색 트리로 변환한다.
3. 루트 노드의 오른쪽 서브트리는 arr의 오른쪽 절반을 이진 검색 트리로 변환한다.
4. 이 과정을 각 서브트리에 대해 재귀적으로 반복
   (배열의 길이가 짝수일경우 앞에 존재하는 데이터를 기준으로 한다.)

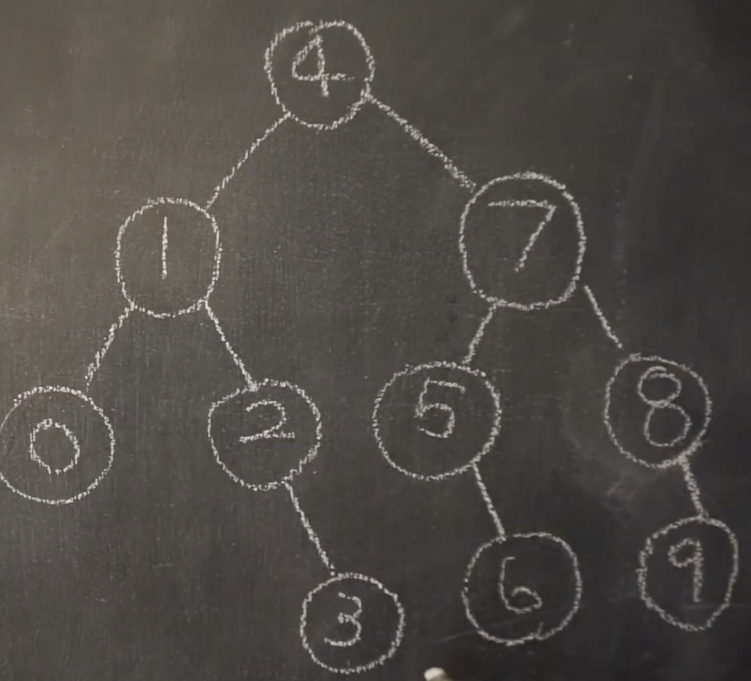
class Tree{ 	
	class Node {     	
    	int data;         
        // 왼쪽 오른쪽 Node를 저장한 변수 선언         
        Node left;         
        Node right;         
        // 생성자에서 데이터를 받아 노드에 저장한다.         
        Node (int data){         	
        	this.data = data;         
        }     
     }      
     
     // Tree 멤버 변수(Tree가 시작되는 root 변수 선언)     
     Node root;          
     
     /* 배열 정보를 받아 트리를 만드는 일을 시작해주는 함수 선언     
      *  이 함수는 재귀 호출을 반복적으로 실행하기 전     
      *  재귀 호출에 필요한 정보를 처음으로 던져주는 역할을하고     
      *  재귀 호출이 끝나면 가장 꼭대기에 있는 루트 노드의 주소를 받아서 멤버 변수에 저장한다.     
      */     
      
     public void makeTree(int[] a){     	
     	root = makeTreeR(a, 0, a.length -1);     
     }          
        // 재귀함수 선언, 인자 : 배열 정보, 시작 인덱스, 끝 인덱스     
        
     public Node makeTreeR(int[] a, int start, int end) {
     /* 시작 인덱스가 끝 인덱스보다 커질 경우 재귀 종료         
     (끝나는 지점을 명확히 해주는게 재귀 호출의 가장 중요한 부분이다.)
     */      	
     	if(start > end) return null;         
        // 받은 시작 지점과 끝 지점으로 중간 지점 계산         
        int mid = (start + end) / 2;         
        // 중간 지점으로 받은 값으로 노드 생성         
        Node node = new Node(a[mid]);  
        
        /* 재귀 호출         
         *  left : 시작 값(0)부터 중간 값 - 1 까지 탐색         
         *  right : 중간 값 + 1 부터 마지막 값 까지 탐색         
         */         
        
        node.left = makeTreeR(a, start, mid-1);         
        node.right = makeTreeR(a, mid+1, end);                  
        return node;     
      }     
      
      /* 트리가 잘 만들어졌는지 확인하는 이진 검색 함수 생성 	 
       * 검색 시작 노드와 찾을 값을 함수 인자로 받는다.      
       * 만약 찾는 값이 Node.data보다 작을 경우 조건문에 의해 왼쪽 트리를 탐색하고      
       * 더 크다면 오른쪽 트리를 탐색하는 과정을 반복한다.     
       */     
     public void searchBTree(Node n, int find) {     	
     	if(find < n.data) {         	
        	System.out.println("Data is smaller than " + n.data);             
            searchBTree(n.left, find);         
         }else if(find > n.data){        		
         	System.out.println("Data is bigger than " + n.data);             
            searchBTree(n.right, find);        
         }else{        	    
         	System.out.println("Data found!");        
         }     
       } 
  }  
  
  public class Test{ 	
  	public static void main (String[] args){     	
    	int[] a = new int[10];         
        for(int i=0; i<a.length; i++){         	
        		a[i] = i;         
         }                  
        
        Tree t = new Tree();         
        t.makeTree(a);         
        t.searchBTree(t.root, 2);     
    } 
}  

결과 : Data is smaller than 4 Data is bigger than 1 Data found!

---