Algorithms

빅오(Big-O) 표기법

onddd 2023. 9. 28. 22:40

728x90

Big-O

Big-O는 알고리즘의 성능을 수학적으로 표기해주는 표기법으로 시간과 공간 복잡도를 표현할 수 있다. Big-O 표기법은 알고리즘의 실제 러닝 타임을 표시하기보다 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는게 목표이기 때문에 상수와 같은 숫자는 모두 1이 된다.

알고리즘은 궁극적으로는 컴퓨터로 구현되므로, 컴퓨터의 빠른 처리 능력을 감안하면 아무리 복잡한 알고리즘도 입력의 크기가 작으면 금방 끝나버린다. 그러므로 관심의 대상이 되는 것은 입력의 크기가 충분히 클 때다. 충분히 큰 입력에서는 알고리즘의 효율성에 따라 수행 시간이 크게 차이가 날 수 있다.

빅오(O, big-O)란 입력값이 무한대로 향할 때 함수의 상한을 설명하는 수학적 표기 방법이다.

시간 복잡도(Time Complexity)의 사전적 정의는 어떤 알고리즘을 수행하는 데 걸리는 시간을 설명하는 계산 복잡도(Computational complexity)를 의미하며 계산 복잡도를 표기하는 대표적인 방법이 바로 빅오다. 빅오로 시간 복잡도를 표현할 때는 최고차항만을 표기하며, 계수는 무시한다. 예를 들어 입력값 n에 대해

번 만큼 계산하는 함수가 있다면 이 함수의 시간 복잡도는 최고 차항만 고려하고 이 중에서도 계수는 무시해 만을 고려 한다. 즉 여기서의 시간 복잡도는 이 된다. 이처럼 시간 복잡도를 표기할 때는 입력값에 따른 알고리즘의 실행 시간의 추이만을 살피게 된다.

O(1) - Constant Time

F(int[] n) { 	
	return (n[0] == 0) ? true : false; 
}

입력 데이터의 크기와 상관 없이 항상 일정한 시간이 걸리는 알고리즘을 말한다.
예시 코드를 살펴보면 배열 n[0]의 값이 0인지 확인하는 코드로 항상 일정한 시간이 걸린다.

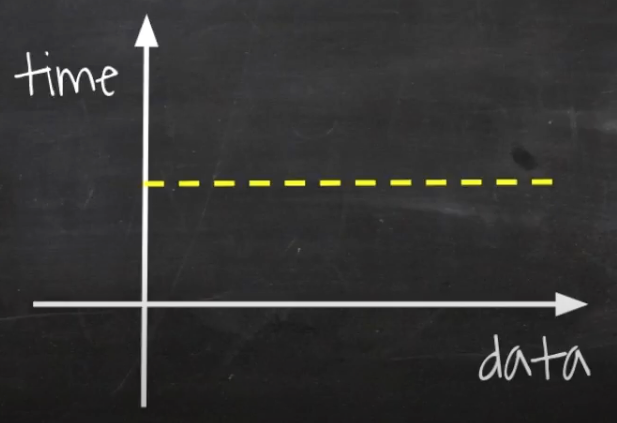
상수 시간을 갖는 알고리즘은 항상 일정한 시간을 보장하기 때문에 최고의 알고리즘이라 할 수 있지만 현실적으로 어려움이 따른다.

또 한 상수 시간에 실행된다 해도 상수값이 상상을 넘어설 정도로 매우 크다면 사실상 일정한 시간의 의미가 없다.

O(1)에 실행되는 알고리즘으로 해시 테이블의 조회 및 삽입이 이에 해당한다.

O(n) - Linear Time

F(int[] n) { 	
  for i = 0 to n.length  
      print i 
 }

O(n) 알고리즘은 입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘을 표현한다. 예를 들어 배열을 순회하는 반복문은 배열의 크기가 커짐에 따라 처리 시간이 늘어난다.

언제나 데이터와 시간이 함께 증가하기 때문에 그래프의 선이 우상향한다.
이러한 알고리즘을 선형 시간(Linear-Time)알고리즘이라고한다. 정렬되지 않은 리스트에서 최댓값 또는 최솟값을 찾는 경우가 이에 해당하며 이 값을 찾기 위해서는 모든 입력값을 적어도 한 번 이상은 살펴봐야 한다.

- Quadratic Time

F(int[] n) { 	
   for i = 0 to n.length     	
      for j = 0 to n.length         	
         print i + j; 
}

n으로 루프를 돌면서 그 안에서 다시 n으로 루프를 돌게되면 만큼의 시간이 소요된다.

첫 번째 루프에서 n개의 데이터를 받으면 첫 번째 루프에서 n번 돌면서 각각의 엘리먼트에서 n번씩 다시 반복하기 때문에 처리 횟 수가 n을 가로, 세로, 길이로 가지는 면적만큼 들게된다.

만약 n이 커진다면 커진만큼 가로, 세로가 늘어나기 때문에 데이터가 커지면 커지는만큼 처리 시간의 부담도 커진다.

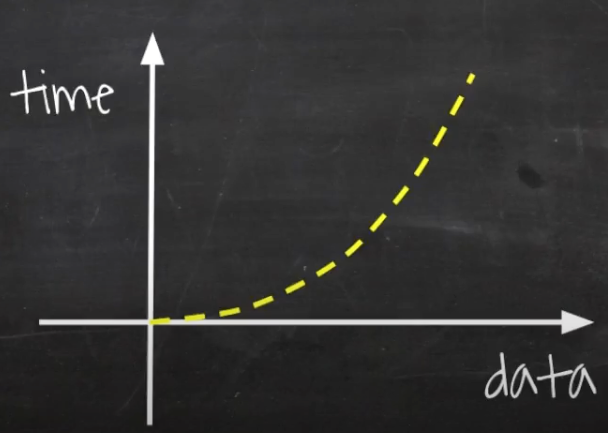
버블 정렬 같은 비효율적인 정렬 알고리즘이 이에 해당한다.

O(nm) - Quadratic Time

F(int[] n, int[] m) { 	
   for i = 0 to n.length     	
      for j = 0 to m.length         	
         print i + j ; 
}

의 코드와 유사하지만 n을 두 번 돌리는게 아닌 m을 n만큼 돌린다. 단순히 루프가 중첩되어 있는것만 보고 의 시간이 걸린다고 착각하기 쉬운데,m의 크기에 따라 크기가 달라지기 때문에 이 부분 주의가 필요하다.

O(nm)도 데이터가 증가할 수록 그래프가 가파르게 올라가는 특징을 가지고 있다.

- Polynomial(cubic) time

F(int[] n) { 	
   for i = 0 to n.length     	
      for j = 0 to n.length         	
         for j = 0 to n.length             	
            print i + j + k; 
}

코드에서 보이는것과 같이 n을 삼 중으로 돌리게되면 만큼의 시간이 소요된다. O(n)은 직선, 이 면적이었다면 은 큐빅 즉, 3차원이 된다.

데이터가 증가함에 따라 소요 시간은 O(n^2)에 비해 더 급격하게 수직 상승하게된다.

- Exponential Time

Finonacci 수열의 재귀적 표현이 대표적인 의 소요 시간을 갖는 자료 구조로 아래 이미지와 같이 1부터 시작해 한 면을 기준으로

새로운 정사각형을 만들어가는 수열이다.

이런 과정을 반복하게 되면 다음과 같은 피보나치 나선형이 그려진다.

F(n, r) { 	
   if (n <= 0) return 0;     
   else if (n == 1) return r[n] = 1;     
   
   return r[n] = F(n - 1, r) + F(n - 2, r); 
}  	->	1, 1, 2, 3, 5 , 8 ...

피보나치 수열을 재귀로 구현하게 되면 함수를 호출할 때 마다 바로 전의 숫자와, 전전 숫자를 알아야하기 때문에 현재 숫자에서 1만큼 뺀

숫자와 2만큼 뺀 숫자를 다시 호출하는 과정을 갖는다.

이렇게 매 번 함수가 호출될 때 마다 두 번씩 다시 호출하는데, 이를 트리의 높이만큼 반복한다.

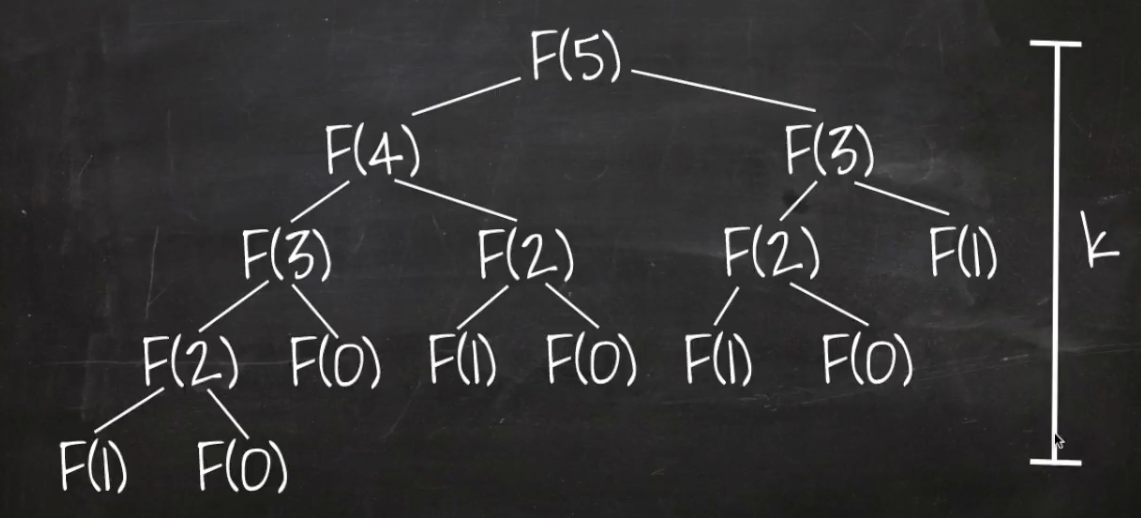
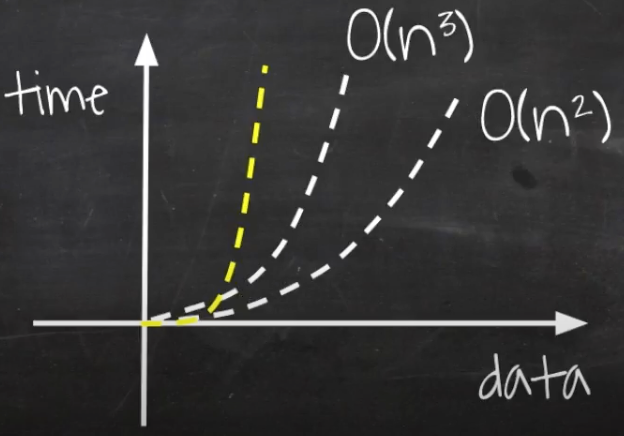
소요 시간은 보다 더 가파르게 증가한다는 특징을 가지고 있다.

그 밖에 m개 씩 번 늘어나는 알고리즘은 다음과 같이 표기한다.

- Exponential Time

O(log n) - Binary Search

O(log n)의 대표적인 알고리즘으로 이진 검색이 있다.

오름차순으로 정렬된 배열에서 '6’을 이진 검색으로 찾는다면 다음과 같은 과정을 갖는다.

배열의 중앙 값을 확인한다.
만약 Key 값이 중앙 값보다 더 크다면 중앙 값 + 1 부터 끝 번까지가 다음 탐색 대상이 된다.
다시 중앙 값 + 1 부터 끝 번의 중앙 값을 확인한다.
Key 값을 찾을때 까지 위 과정을 반복한다.

이렇게 한 번 탐색 할 때마다 검색 대상이 절반씩 줄어드는 알고리즘을 O(log n) 알고리즘이라고 한다.

F(k, arr, s, e) { 	
   if(s > e) return -1;     
   m = (s + e) / 2;     
   if(arr[m] == k) return m;     
   else if (arr[m] > k) return F(k, arr, s, m-1);     
   else return F(k, arr, m+1, e); 
}

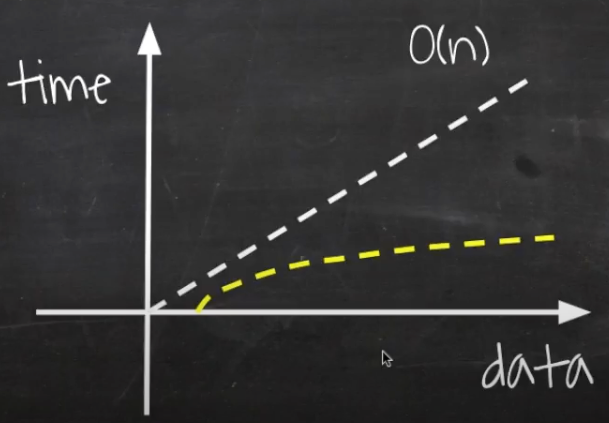
O(log n)은 O(n) 보다도 속도가 빠르고 데이터의 양이 늘어나더라도 성능이 크게 차이나지 않는다.

O(n log n)

병합 정렬을 비롯한 대부분의 효율 좋은 정렬 알고리즘이 이에 해당한다.

적어도 모든 수에 대해 한 번 이상은 비교해야 하는 비교 기반 정렬 알고리즘은 아무리 좋은 알고리즘도 (O n log n)보다 빠를 수 없다.

물론 입력 값이 최선인 경우, 비교를 건너뛰어 O(n)이 될 수 있다.

O(n!)

각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 외판원 문제를 브루트 포스로 풀이할 때가 이에 해당하며 가장 느린 알고리즘으로 입력값이 조금만 커져도 웬만한 다항 시간 내에는 계산이 어렵다.

O(sqrt(n))

대표적으로 소수 판정 알고리즘이 O(sqrt(n)) 시간 복잡도를 가진다.
자연수 N이 소수임을 판별하는 방법은 크게 두 가지가 있다.

2부터 n-1까지의 자연수로 자연수 N을 나눴을 때 나누어 떨어지는지 보는 방법
sqrt(N)까지만 나누면서 소수임을 판별하는 방법

첫 번째 방법은 n-1 까지의 수를 모두 확인해야하므로 O(N)의 시간 복잡도를 갖지만
제곱근을 사용하는 두 번째 방법은 모든 수가 아닌 제곱근까지 확인하기 때문에 O(sqrt(n))의 시간 복잡도를 갖게된다.

이를 정사각형의 박스로 두고 본다면 1행에 해당하는 부분이 제곱근이될것이다.

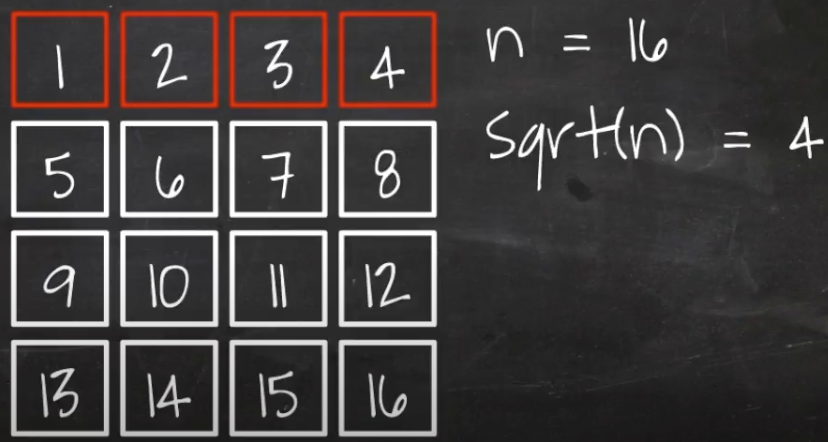
Drop Constants

Big-O에선 상수를 과감하게버린다.

F(int[] n) { 	
   for i = 0 to n.length     	
      print i     
        for i = 0 to n.length     	
          print i 
 }

위 코드와 같은 메서드가 존재할 때 상수를 제거하지않고 그대로 표기한다면 O(2n)의 시간 복잡도를 갖지만 Big-O에선 상수를 제거하기 때문에 O(n)으로 표기하는것이다.

그 이유로 Big-O 표기법은 알고리즘의 러닝 타임을 체크하기 위해 사용하는것이 아닌 장기적으로 데이터가 증가함에 따른 처리 시간의 증가율을 예측하기 위해 사용하기 때문이다.

차원이 늘어나지않는한 동일한 시간 복잡도를 가진 알고리즘은 모두 상수를 제거하고 표기하는게 원칙이다.

추가

빅오는 시간 복잡도 외에도 공간 복잡도를 표현하는 데에도 널리 쓰인다.

또 한 알고리즘은 흔히 ‘시간과 공간이 트레이드 오프(Space-Time Tradeoff)’관계라고도 하는데 이 말은 실행 시간이 빠른 알고리즘은

공간을 많이 사용하고, 공간을 적게 사용하는 알고리즘은 실행 시간이 느리다는 얘기다.

물론 실행 시간이 빠르면서도 공간을 적게 차지하는 알고리즘이 존재하지만 대부분의 경우 시간과 공간은 트레이드오프 관계이며

이는 알고리즘의 주요한 특징 중 하나이다.

상한과 최악

빅오(O)는 상한(Upper Bound)을 의미한다. 이외에도 하한(Lower Bound)을 나타내는 빅오메가, 평균을 의미하는 빅세타가 있는데,

학계와 달리 업계에서는 빅세타와 빅오를 하나로 합쳐 단순화해 표현하려는 경향이 있다.

평균적인 시간보다는 상한 시간으로 단순화하여 주로 표현하는데,  
매번 구분하는것이 번거롭고 혼동되기도 하며 상한으로만 표현하는 방법이 틀리지 않기 때문이다.  
여기서 한 가지 중요한 점은 상한을 최악의 경우와 혼동하는 것인데,  
빅오 표기법은 정확하게 쓰기에는 너무 길고 복잡한 함수를 ‘적당히 정확하게’  표현하는 방법일 뿐, 
최악의 경우,평균적인 경우의 시간 복잡도와는  아무런 관계가 없는 개념이라는 점에 유의해야한다.

분할 상환 분석

분할 상환 분석(Amortized Analysis)은 빅오와 함께 함수의 동작을 설명할 때 중요한 분석 방법 중 하나로 분할 상환 분석이 유용한

대표적인 예로 ‘동적 배열’을 들 수 있는데, 동적 배열에서 더블링이 일어나는 일은 어쩌다 한 번 뿐이지만, 이로 인해

‘아이템 삽입 시간 복잡도는 O(n)이다’ 라고 확정짓는건 지나치게 비관적이고 정확하지도 않다.

따라서 이 경우 ‘분활 상환’ 또는 ‘상각’ 이라고 표현하는, 
최악의 경우를 여러 번에 걸쳐 골고루 나눠주는 형태로 알고리즘의 시간 복잡도를 계산할 수 있다. 
이렇게 할 경우 동적 배열의 삽입 시 시간 복잡도는 O(1)이 된다.

병렬화

일부 알고리즘들은 병렬화로 실행 속도를 높일 수 있다.
딥러닝의 인기와 함께 병렬화가 큰 주목을 받고 있으며 GPU는 병렬 연산을 위한 대표적인 장치이기도 하다.

GPU는 결국 같은 시간에 훨씬 더 많은 연산을 할 수 있기 때문에 딥러닝 알고리즘을 비롯해  
병렬 연산이 가능한 알고리즘들은 최근에 큰 주목을 받고 있다.  
알고리즘 자체의 시간 복잡도 외에도 알고리즘이 병렬화가 가능한지는 
근래에 알고리즘의 우성을 평가하는 매우 중요한 척도 중 하나이기도 하다.

책 파이썬 알고리즘 인터뷰, 유튜브 엔지니어대한민국 님의 [자료구조 알고리즘] 빅오(Big-O)표기법 완전정복 영상의 내용을 기록한 포스트입니다.