Graph에 대해
그래프(Graph)와 트리(Tree)는 모두 노드(Node)와 노드를 연결하는 간선(Edge)으로 구성된 자료 구조이지만 몇 가지 차이점이 존재한다.
- 순환(cycle)의 존재 여부
그래프는 순환을 가질 수 있지만, 트리는 순환을 가질 수 없다. 트리는(DAG, Directed Acyclic Graph)라고도 부른다. - 루트(Root)의 존재 여부
- 트리는 하나의 루트 노드를 가지며, 모든 노드는 루트 노드로부터 유일한 경로로 연결된다. - 그래프에는 루트 노드가 없다. - 간선의 방향성
그래프의 간선은 양방향일수도 있고, 단방향일수도 있지만 트리는 단방향이다. - 연결성
그래프에서는 연결성(Connectivity)이 중요한 개념이지만, 트리에서는 연결성이 보장된다. 즉, 트리는 모든 노드가 연결되어 있어서 어떤 노드에서도 다른 노드로 이동할 수 있다. - 노드의 차수
그래프에서는 노드의 차수(Degree)가 제한이 없지만, 트리에서는 루트 노드를 제외하면 모든 노드의 차수가 1 이상이고, 리프(Leaf) 노드는 차수가 0이다. 그래프와 트리는 노드와 간선으로 구성된 자료 구조이지만, 트리는 그래프의 특수한 경우로, 특정한 규칙을 가지기 때문에 사용하는 목적에 따라 선택하여 사용된다.
(트리는 그래프의 한 형태이다.)
Graph
그래프는 노드와 노드를 연결하는 간선으로 구성된 추상적인 자료 구조로 노드는 정점(Vertex)이라고도 부른다.
방향성(Directed)과 가중치(Weighted)의 유무에 따라 여러 가지 유형으로 분류할 수 있다.
무방향 그래프(Undirected Graph)
간선의 방향성이 없는 그래프를 의미한다.
( 노드 사이의 연결 관계가 양방향으로 존재한다.)
A -- B -- C
| |
D -- E -- F이 그래프는 A,B,C,D,E,F 총 6개의 노드와 이들 노드를 연결하는 7개의 간선으로 이루어져 있고, 간선의 방향이 없으므로 각 노드는 양방향으로 연결되어 있다.A와B는 양방향으로 연결되어 있으며, B와C도 양방향으로 연결되어 있다.
같은 방식으로 D와E, E와F도 양방향으로 연결되어있다.
방향 그래프(Directed Graph)
간선의 방향성이 있는 그래프를 의미한다.
( 노드 사이의 연결 관계가 단방향으로 존재한다. )
A -> B -> C
| |
v v
D <- E <- FA, B, C, D, E, F 총 6개의 노드와 이들 노드를 연결하는 6개의 간선으로 이루어져 있다. 간선은 방향성이 있으므로, A에서 B로 가는 간선은 B에서 A로 가는 간선과 다르다.
A에서B로 가는 간선은 존재하지만, B에서 A로 가는 간선은 없고, 같은 방식으로 F에서 E로 가는 간선은 존재하지만 E에서 F로 가는 간선은 없다.
방향 그래프에서 간선의 방향성이 중요하므로, 간선의 방향성으로 인해, 어떤 노드는 다른 노드로 가는 간선이 있어도 다른 노드로부터 오는 간선이 없을 수 있다.
(트리는 Directed Graph에 속한다)
가중치 그래프(Weighted Graph)
간선에 가중치가 할당된 그래프를 의미한다. 가중치는 엣지를 통해 연결된 노드 사이의 거리, 비용, 시간 등을 나타낸다.
5
A--------B
|\ /|\
| \ 2 / | \
7 | \ / | \ 1
| \/ | \
| /\ | /
6 | / \ | / 3
| / 3 \ | /
|/ \|/
D--------C
4A,B,C,D 총 4개의 노드와 이들 노드를 연결하는 8개의 간선으로 이루어져 있다.
간선은 가중치를 가지므로 각각의 간선에는 그에 해당하는 가중치가 표시된다.
A와 B를 연결하는 간선은 가중치가 5이고, D와 A를 연결하는 간선은 가중치가 7이다.
방향 가중치 그래프(Directed Weighted Graph)
간선에 방향성과 가중치가 모두 할당된 그래프를 의미한다.
1 -5-> 3 -2->
A <--- / \ ---> D
^ / 2 / \ -1 ^
-6| / / \ |5
| / / \ |
|/ / \ |
B / \ C
^ / 3 4 \ v
-3| / \ |
| / \|
-----------------------
2A,B,C,D 네 개의 노드와 이들 노드를 연결하는 간선 7개로 이루어져있는 그래프이다.
간선은 방향성을 가지며, 각각의 간선에는 그에 해당하는 가중치가 표시된다.
Graph 표현 방법
Adjacency Matrix (인접 행렬)
2차원 배열로 그래프를 표현하는 방법으로 배열의 인덱스는 노드를 나타내며, 배열의 값은 노드 간의 연결 여부를 나타낸다.
무방향 그래프의 경우, 배열은 대칭성을 가진다. 간선의 존재 여부를 빠르게 확인할 수 있지만, 그래프가 sparse한 경우 메모리 낭비가 발생할 수 있다.
A
/ | \
B | C
\ | /
D
A B C D
+---------
A | 0 1 1 1
B | 1 0 0 0
C | 1 0 0 1
D | 1 0 1 0A,B,C,D 네 개의 노드와 이들을 연결하는 간선 5개로 이루어진 그래프이다. 각각의 노드는 그래프의 열과 행으로 대응되며, 간선이 존재하면 해당 위치에 1을, 존재하지 않으면 0을 표시한다. 예로 A와B 사이에 간선이 존재하므로 인접 행렬에서는 1로 표시된다.
그래프가 sparse 하다는 것은, 그래프의 간선의 수가 노드의 수에 비해 상대적으로 매우 작다는 것을 의미한다.
(그래프에서 실제로 존재하는 간선의 수가 전체 가능한 간선의 수보다 매우 작은 경우)
예를 들어 n개의 노드가 있는 그래프에서 간선의 개수가 O(n)보다 작은 경우 그래프는 대부분의 노드 쌍 사이에는 간선이 없는 sparse한 그래프이다.
반대로 간선의 수가 노드의 수에 비해 매우 많은 경우 dense한 그래프라고 한다.
Adjacency List (인접 리스트)
인접 리스트는 연결 리스트로 그래프를 표현하는 방법이다.
리스트의 인덱스는 노드를 나타내며, 리스트의 값은 해당 노드와 인접한 노드들을 나타낸다. (sparse한 그래프를 표현하는데 적합하다.)
각 노드의 인접한 노드를 순회하면서 간선의 존재 여부를 확인해야 하므로 인접 행렬에 비해 상대적으로 느린 성능을 보일 수 있다.
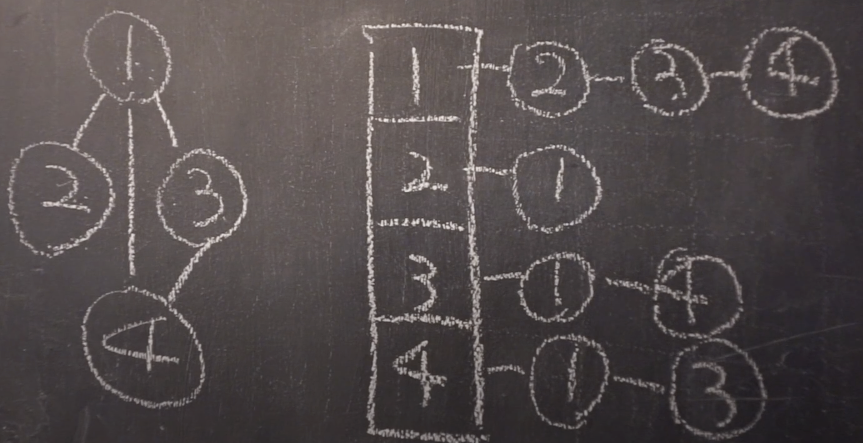
인접 리스트 그래프는 무방향 그래프를 나타내며, 각 노드의 리스트는 일방향으로만 표시된다.
이는 인접 리스트 그래프의 특징 중 하나이다. 주로 LinkedList를 통해 구현한다.그래프는 이러한 유형을 기반으로 다양한 문제를 해결하는 데 사용된다. 대표적인 예로는 최단 경로 찾기, 네트워크 흐름, 트리 찾기, 사이클 검사 등이 있고, 그래프는 데이터베이스, 자연어 처리, 컴퓨터 비전 등 다양한 분야에서도 활용되고 있다.
