Graph 검색 구현
그래프를 검색하는 방법은 대표적으로 깊이 우선 검색(Depth-First Search, DFS),넓이 우선 검색(Breadth-First Search, BFS)가 있다.
DFS
DFS는 이진 트리를 순회할 때 사용했던 inorder, preorder, postorder 순회 방법이 깊이 우선 검색에 속하는데 시작 노드에서 자식 노드로 탐색을 진행하다 더 이상 탐색할 자식 노드가 없으면 부모 노드로 돌아가 다음 자식 노드를 탐색하고 이 과정을 반복해 그래프를 끝까지 탐색하게된다.
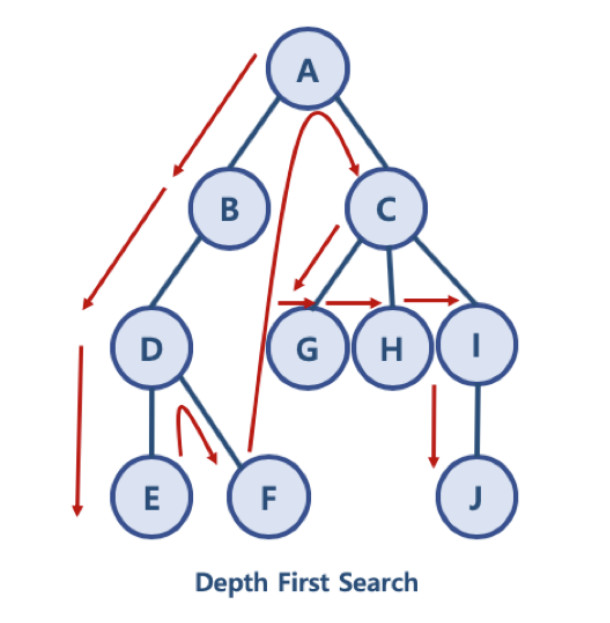
DFS는 모든 노드를 탐색하며, 각 노드를 한 번씩 방문한다. DFS는 그래프에서 연결된 모든 노드를 방문할 수 있으며, 이를 통해 그래프의 구조를 파악하는데 도움이 된다. 또한, 그래프에서 경로를 찾거나 사이클을 검사하는데 사용할 수 있다.
BFS
BFS(Breadth-First Search)는 그래프 탐색 알고리즘 중 하나로, 시작 노드에서부터 거리가 가까운 노드부터 탐색하는 방법이다.
즉, 시작 노드에서 인접한 노드를 먼저 모두 방문한 후, 방문한 각 인접 노드에서 또 다시 인접한 노드를 모두 방문하는 방식으로 탐색을 진행한다. (레벨 단위로 탐색이 진행된다.)
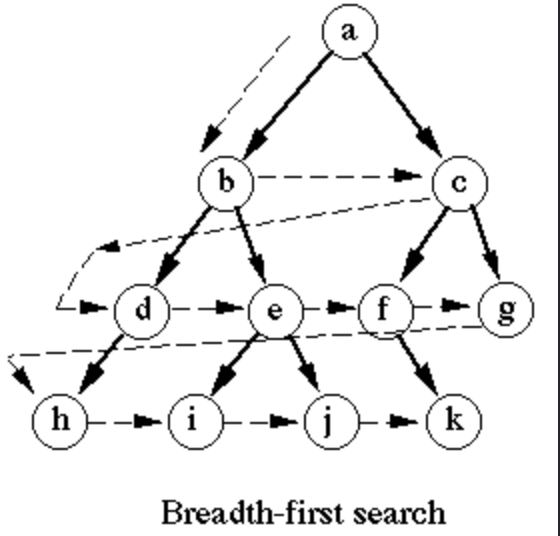
특징
탐색 순서
DFS는 시작 노드에서부터 깊이 우선으로 탐색을 진행한다. 인접한 노드 중 하나를 선택하고, 선택한 노드에서 또 다시 깊이 우선으로 탐색을 진행하는데 이러한 방식으로 탐색을 진행하다가 더 이상 탐색할 수 없는 상황에 도달하면, 이전에 방문한 노드로 돌아가서 다른 인접 노드를 선택하여 탐색한다.
BFS는 시작 노드에서부터 너비 우선으로 탐색을 진행한다. 시작 노드에서 인접한 노드를 먼저 모두 방문한 후, 방문한 각 인접 노드에서 또 다시 인접한 노드를 모두 방문하는 방식으로 탐색한다.
사용하는 자료구조
DFS는 스택(Stack)이나 재귀 함수를 사용하여 구현할 수 있다. 시작 노드에서부터 탐색을 시작하며, 탐색 경로 상의 노드들을 스택에 push한 후, 더 이상 탐색할 수 없는 상황에 도달하면 스택에서 pop하여 이전에 방문한 노드로 돌아가서 다른 경로를 탐색합니다.
BFS는 큐(Queue)를 사용하여 구현한다. 시작 노드를 큐에 push한 후, 큐에서 노드를 하나씩 꺼내어 그 노드의 인접 노드를 큐에 push하고 방문 처리합니다. 이 과정을 큐가 빌 때까지 반복한다.
탐색 시간
DFS는 탐색 경로 상에 있는 모든 노드를 탐색하기 때문에, 탐색 시간이 느릴 수 있다. 최악의 경우, 모든 노드를 방문해야 하므로 시간 복잡도는 O(V+E)가 된다.
BFS는 너비 우선으로 탐색하기 때문에, 최단 경로를 탐색하는 경우에는 DFS보다 빠른 속도로 결과를 찾을 수 있습니다. 시간 복잡도는 DFS와 마찬가지로 O(V+E)이다.
DFS와 BFS의 시간 복잡도는 그래프의 크기(V+E)에 비례한다. V는 노드의 개수, E는 간선의 개수로 DFS는 모든 노드를 방문하고, 각 노드를 한 번씩 방문하므로 시간 복잡도는 O(V+E)가 된다.
구현
DFS-Stack
스택 자료구조를 사용해 시작 노드에서부터 DFS 탐색을 수행하고, 각 노드를 출력하는 간단한 예시 코드이다.
import java.util.Stack;
class Graph {
private int V; // 노드의 개수
private LinkedList<Integer>[] adj; // 인접 리스트
// 그래프 초기화
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// 노드를 연결 v->w
void addEdge(int v, int w) {
adj[v].add(w);
}
// DFS 탐색
void DFS(int s) {
boolean[] visited = new boolean[V];
Stack<Integer> stack = new Stack<>();
visited[s] = true;
stack.push(s);
while (!stack.isEmpty()) {
s = stack.pop();
System.out.print(s + " ");
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
stack.push(n);
}
}
}
}
}Graph 클래스에서 DFS 메서드를 사용하여 DFS 탐색을 구현한다.
DFS 메서드는 시작 노드 s를 매개변수로 받으며, 내부에서는 boolean 배열 visited와 Stack 자료구조를 사용하여 탐색을 수행
먼저 visited 배열을 초기화한 후, 시작 노드를 Stack에 push하고 Stack이 빌 때까지 다음을 반복한다.
- Stack에서 노드를 pop하고, 해당 노드를 출력
- 해당 노드의 인접 노드를 확인하고, 아직 방문하지 않은 인접 노드는 visited 배열에 방문 처리를 하고 Stack에 push
DFS-Recursion
재귀 호출을 통해 Graph 클래스에서 DFS 메서드와 DFSUtil 메서드를 사용하여 DFS 탐색을 구현하는 코드로
시작 노드에서부터 DFS 탐색을 수행하고, 각 노드를 출력하는 간단한 예시이다.
import java.util.*;
class Graph {
private int V; // 노드의 개수
private LinkedList<Integer>[] adj; // 인접 리스트
// 그래프 초기화
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// 노드를 연결 v->w
void addEdge(int v, int w) {
adj[v].add(w);
}
// DFS 탐색
void DFSUtil(int v, boolean[] visited) {
visited[v] = true;
System.out.print(v + " ");
Iterator<Integer> i = adj[v].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n])
DFSUtil(n, visited);
}
}
// DFS 탐색
void DFS(int v) {
boolean[] visited = new boolean[V];
DFSUtil(v, visited);
}
}DFS 메서드는 시작 노드 v를 매개변수로 받으며, 내부에서는 boolean 배열 visited를 초기화한 후, DFSUtil 메서드를 호출한다.
DFSUtil 메서드는 현재 노드 v와 visited 배열을 매개변수로 받는데 먼저 현재 노드를 방문 처리하고, 해당 노드를 출력한다.
그리고 해당 노드의 인접 노드를 확인하면서, 아직 방문하지 않은 인접 노드는 visited 배열에 방문 처리를 하고 DFSUtil 메서드를 재귀적으로 호출한다.
BFS
코드는 그래프가 주어졌을 때, 시작 노드에서부터 BFS 탐색을 수행하고, 각 노드를 출력하는 예시 코드이다.
import java.util.*;
class Graph {
private int V; // 노드의 개수
private LinkedList<Integer>[] adj; // 인접 리스트
// 그래프 초기화
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i){
adj[i] = new LinkedList();
}
}
// 노드를 연결 v->w
void addEdge(int v, int w) {
adj[v].add(w);
}
// BFS 탐색
void BFS(int s) {
// 방문 여부를 나타내는 배열
boolean[] visited = new boolean[V];
// BFS에 사용할 큐
LinkedList<Integer> queue = new LinkedList<Integer>();
// 시작 노드 방문 처리 및 큐에 삽입
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
// 큐에서 노드를 꺼내와 방문 처리
s = queue.poll();
System.out.print(s + " ");
// 꺼낸 노드의 인접 노드 중 방문하지 않은 노드를 큐에 삽입
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
}Graph 클래스에서 BFS 메서드를 사용하여 BFS 탐색을 구현하고 있다.
BFS 메서드는 시작 노드 s를 매개변수로 받으며, 내부에서는 boolean 배열 visited를 초기화한 후, 큐를 초기화한다.
시작 노드를 방문 처리하고 큐에 삽입한 후, 큐가 비어있을 때까지 반복적으로 아래 과정을 수행한다.
- 큐에서 노드를 꺼내와 방문 처리
- 꺼낸 노드의 인접 노드 중 방문하지 않은 노드를 큐에 삽입
통합 구현 엔지니어 대한민국
import java.util.LinkedList;
import java.util.Iterator;
import java.util.Stack;
import java.util.NoSuchElementException;
class Queue<T>{ }
class Graph{
class Node{
int data;
// 인접한 노드들과의 관계
LinkedList<Node> adjacent;
// 방문했는지 마킹
boolean marked;
//Node 생성자
Node (int data){
this.data = data;
this.marked = false;
adjacent = new LinkedList<Node>();
}
}
Node[] nodes; // node들을 저장할 배열
Graph(int size){
nodes = new Node[size];
for(int i=0; i<size; i++){
nodes[i] = new Node(i);
}
}
//두 노드의 관계를 저장
void addEdge(int i1, int i2){
Node n1 = nodes[i1];
Node n2 = nodes[i2];
//상대방이 있는지 확인하고 없으면 추가
if(!n1.adjacent.contains(n2)){
n1.adjacent.add(n2);
}
if(!n2.adjacent.contains(n1)){
n2.adjacent.add(n1);
}
}
/* Stack을 이용한 DFS 구현*/
void dfs(){
dfs(0);
}
void dfs(int index){
Node root = nodes[index];
Stack<Node> stack = new Stack<Node>();
stack.push(root);
root.marked = true;
while(!stack.isEmpty()){
Node r = stack.pop();
for(Node n : r.adjacent){
if(n.marked == false){
n.marked = true;
stack.push(n);
}
}
visit(r);
}
}
/* 재귀 호출을 이용한 DFS 구현 */
void dfsR(Node r){
if(r==null) return;
r.marked = true;
visit(r);
for(Node n : r.adjacent){
if(n.marked == false){
dfsR(n);
}
}
}
void dfsR(int index){
Node r = nodes[index];
dfsR(r);
}
void dfsR(){
dfsR(0);
}
/* Queue를 이용한 BFS 구현 */
void bfs(){
bfs(0);
}
void bfs(int index){
Node root = nodes[index];
Queue<Node> queue = new Queue<Node>();
queue.enqueue(root);
root.marked = true;
while(!queue.isEmpty()){
Node r = queue.dequeue();
for(Node n : r.adjacent){
if(n.makred == false){
n.marked = true;
queue.enqueue(n);
}
}
visit(r);
}
}
//출력
void visit(Node n){
System.out.print(n.data+" ");
}
}
/*
0
/
1ㅡㅡ3 7
| / | \ /
| / | 5
2ㅡㅡ4 \
6ㅡ8
*/
public class Test{
public static void main(String[] args){
Graph g = new Graph(9);
g.addEdge(0,1);
g.addEdge(1,2);
g.addEdge(1,3);
g.addEdge(2,4);
g.addEdge(3,4);
g.addEdge(3,5);
g.addEdge(5,6);
g.addEdge(5,7);
g.addEdge(6,8);
g.bfs();
g.dfs();
g.dfsR();
}
}

